1. Introducción
El primer tratado de teoría de la música, atribuido a Lasso de Hemíone (siglo VI a.C.) y la experimentación con el monocordio, por parte de Pitágoras (569 a.C. – 475 a.C.), son parte de la producción intelectual multidisciplinar que fueron consecuencia de la intensa actividad académica de su época. A su vez, la escuela pitagórica buscaba los razonamientos numéricos que pudieran dar explicación, desde las matemáticas, a los fenómenos de todo cuanto existe en la naturaleza; además, al fraccionar una cuerda, sentaron los fundamentos primarios de la acústica; y también, integraron la aritmética, la geometría, la música y la astronomía, como parte de los fundamentos científicos en la educación básica[1].
Es así que, los antecedentes anteriormente mencionados, evidencian la constante exploración y desarrollo de elementos conceptuales a partir de la correlación entre disciplinas, lo que plantea su relevancia en la construcción del conocimiento científico. De esta manera, el presente texto pretende realizar un acercamiento abordando las teorías de Ritmos Euclidianos y de Conjuntos de Grados Cromáticos[2], incorporándolas a los elementos expresivos musicales a través de su empalme, de manera que, sean la génesis de posteriores proyectos compositivos, elementos en el análisis teórico, y de manera mas inmediata, una obra para piano como resultado de su estudio y aplicación.
2. El algoritmo de Euclides y el Máximo Común Divisor
Las figuras geométricas fueron de gran relevancia en los tiempos contemporáneos a Pitágoras, debido al apoyo visual que estas producen al momento de resolver ciertas operaciones matemáticas, es asi que, para hallar el algoritmo de Euclides, utilizaban fragmentos procedentes de una recta que permitieran su posterior medición de forma exacta, encontrando la que sería la máxima medida común de ellos. Consecuentemente, se dice que dos segmentos (a, b) y (c, d) son conmensurables cuando se pueden medir de forma exacta con el segmento (e, f) ya que este último, se acomada un número exacto de veces en los primeros[3]. El algoritmo de Euclides consiste justamente en encontrar el segmento (e, f) que sería la medida que divide de forma exacta los segmentos (a, b) y (c, d), a este proceso se le denomina Maximo Común Divisor (MCD).[4]
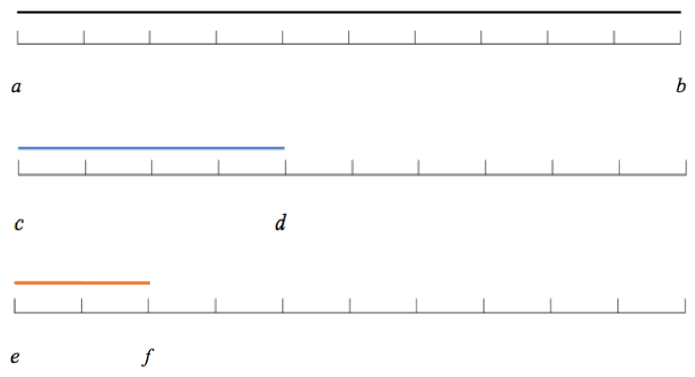
Figura 1: Segmentos conmensurables.
Fue Euclides (325 a.C. – 256 a.C.)[5] quien ideó este método matemático que permite calcular el máximo común divisor (MCD) de dos números enteros mediante un proceso que tiene como base la sucesión de divisiones, empleado la siguiente formula.[6]
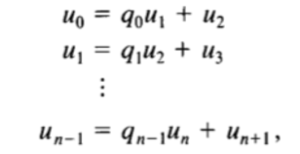
Figura 2: Formula para calcular el MCD. Tomado de[7]
Para calcular el MCD, se asignan valores a los segmentos utilizando dos números enteros cualquiera, es así como, en un supuesto, el primer segmento (a = 87) y el segundo segmento (b = 27). Es por ello que, dados dos números enteros positivos, se procede a calcular el aplicando la siguiente formula[8]:
87 = 27 (3) + 6
27 = 6 (4) + 3
6 = 3 (1) + 3
3 = 3 (1) + 0
El debido a que este número es el último resto que es diferente de cero.
3. Ritmos generados a partir del algoritmo de Euclides
Habiendo conocido el proceso matemático para calcular el MCD por medio del algoritmo de Euclides, se procede a estudiar su aplicación en la música mediante la organización de patrones rítmicos provenientes de este principio matemático.
En primera instancia, en este estudio se implementaran tres tipos de notaciones diferentes a la notación musical convencional, la primera de ellas es la notación de cajas o Box Notation Method, en donde la simbología implementada es: [x ·] las cuales, identifican al ataque y al silencio, respectivamente. El segundo tipo es la notación TUBS, que en su concepto es similar a la anterior, cambiando su forma de ser representada. Finalmente, el tipo de notación Clockwise Distance Sequence Notation, la cual representa geométricamente el desarrollo del patrón rítmico a través del tiempo[9]. En la siguiente tabla, y a modo de ejemplo, es representado un ritmo regular con los tres tipos de notación en el orden que fueron expuestas anteriormente.
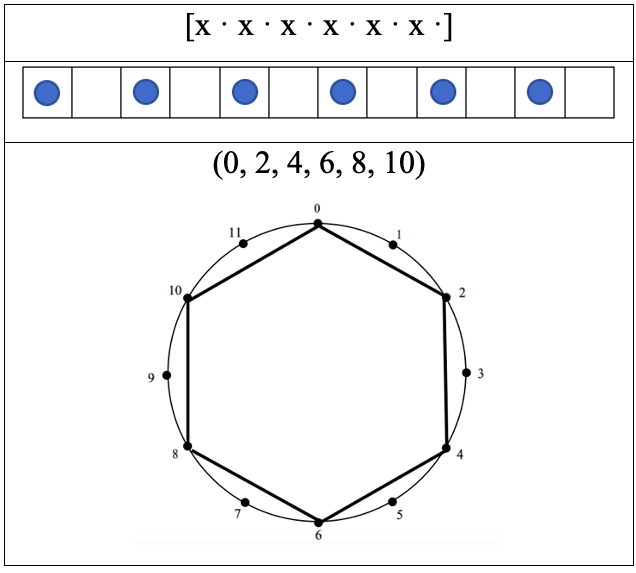
Tabla 1: Representación de un ritmo regular
Los ritmos euclidianos están enmarcados en el denominado principio de regularidad, el cual consiste en distribuir lo más equitativamente posible los ataques en los pulsos y esto solo es posible cuando la división de los pulsos se da con números enteros, por ejemplo: si se quiere tocar 6 ataques en 12 pulsos, se debe dividir 12 entre 2, de tal forma que, su resultado seria: la distribución de 6 ataques a intervalos de 2 pulsos de distancia entre ellos[10].
![]()
Figura 3: Ritmo regular de doce pulsos y seis ataques
Como se aprecia en la imagen anterior, los ataques quedan distribuidos de manera regular en su disposición, todo lo contrario si se quisieran distribuir 8 ataques en 12 pulsos, el número divisor no seria un entero, por lo tanto carecería de regularidad en su distribución, así que los ritmos producidos por el principio de regularidad se denominan ritmos euclideos[11]. En este estudio se tomará el ejemplo E(3,8) que procede del patrón rítmico de la Habanera, con el propósito de desarrollar el proceso para obtener un ritmo euclideo.
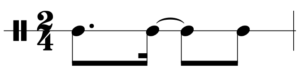
Figura 4: Patrón rítmico de Habanera Cubana
Fue E. Bjorklund, quien idea un método para generar ritmos euclideos, consistiendo en la construcción y distribución de secuencias conformadas por (n) intervalos de tiempo y (k) ataques, siendo estos distribuidos bajo el principio de regularidad y sometidos al siguiente proceso[12]:
- Dados los siguientes valores: n = 8; k = 3, se expresa que: 8 – 3 = 5; por lo tanto, el orden de la secuencia inicial comprende en su estructura a: una fila de 3 unos, seguida de otra fila de 5 ceros. Esta distribución se ejecuta independiente en sus elementos de manera que, se construyan secuencias individuales conformadas por conjuntos de un bit, en este caso la concatenación resultante seria: 8 secuencias de un bit cada una.
[1] [1] [1] [0] [0] [0] [0] [0]
- Distribuir individualmente los ceros en cada secuencia de unos y según su cantidad, de esta manera, se obtienen cinco secuencias, las tres primeras son conjuntos de dos bits y las dos restantes son conjuntos de un bit.
[10] [10] [10] [0] [0]
- De manera similar, se suman individualmente los ceros “sobrantes” y en su orden a las primeras secuencias[13], dando como resultado tres secuencias, las dos primeras son conjuntos de tres bits y una última, un conjunto de dos bits. Como se observa, no quedan ceros sobrantes, asi que es esta la instancia final del proceso.
[100] [100] [10]
- Finalmente, se integran las secuencias del proceso anterior en un solo conjunto, obtieniendo asi una sola secuencia binaria de ocho bits como se aprecia a continuación:
[10010010]
Ahora bien, podria generarse un proceso complemetario en donde la última secuencia [10] se adiera a la primera de la forma siguiente: [10010][100], sin embargo, no implica cambios sustanciales debido a que se trata de secuencias binarias cíclicas, las cuales podrian ser relacionadas o interpretadas como ostinatos rítmicos o claves, por su uniformidad a través del tiempo[14].
Es posible emplear un método que presenta diferencias en su proceso pero no en su resultado, este consiste en agrupaciones verticales en donde los ceros son distribuidos progresivamente debajo y según el número de unos que integre la concatenación ,de manera que, se genere una especie de bloques binarios los cuales, producirán una secuecia final extraida del ordenamiento de sus columnas[15].
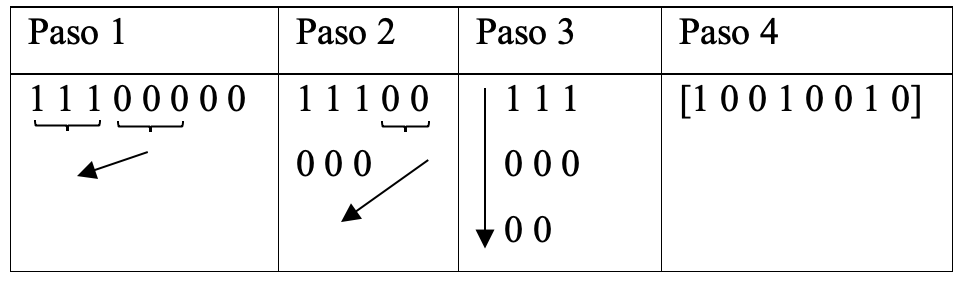
Tabla 2: Proceso para hallar una secuencia binaria
Al obtener la secuencia binaria final, se procede a realizar la transcripción desde el lenguaje matemático, a la escritura musical convencional a través de Box Notation Method, TUBS y Clockwise Distance Sequence Notation, para efectos de posteriores análisis, comparación o clasificación automática de cada patrón rítmico[16].
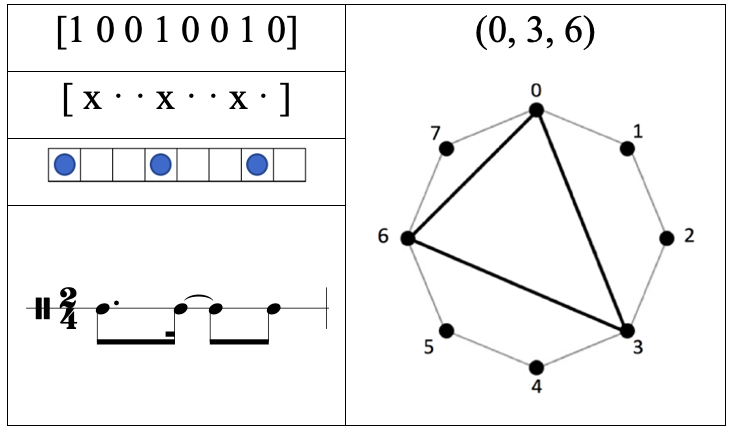
Tabla 3: Representaciones del ritmo E(3,8)
Por medio de los tipos de transcripciones mencionados anteriormente, es posible consultar una extensa clasificación de ritmos como por ejemplo: El E(3, 4) que corresponde al patrón rítmico de la Cumbia de Colombia, o el E(5, 16)[17] perteneciente al patrón rítmico de Bossa-Nova de Brasil[18].
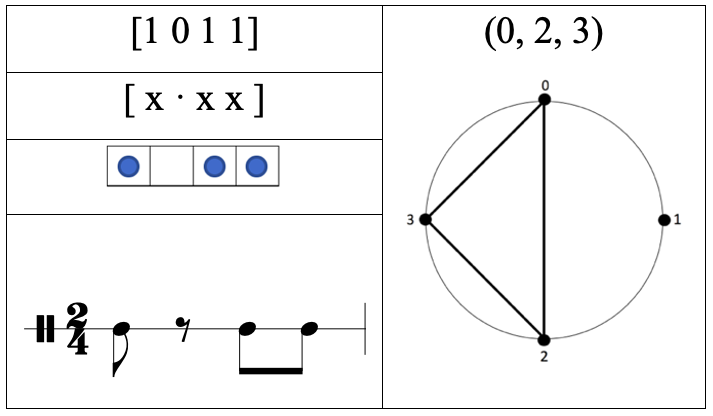
Tabla 4: Representaciones del ritmo E(3,4)
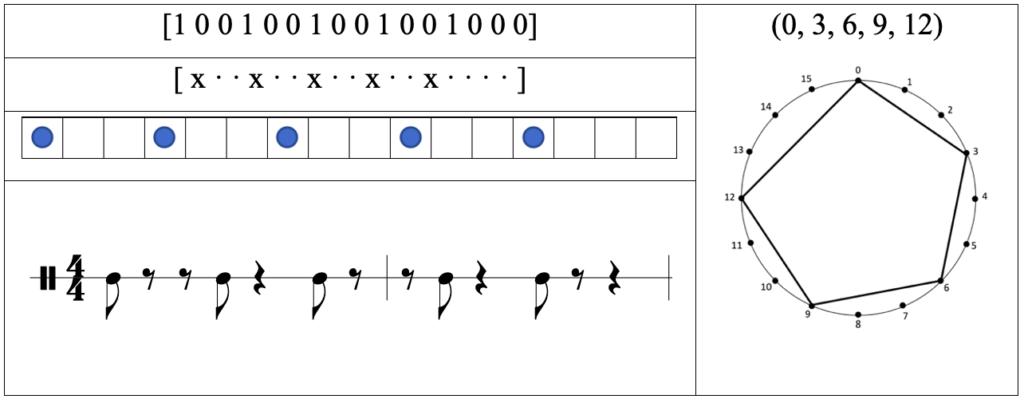
Tabla 5: Representaciones del ritmo E(5,16)
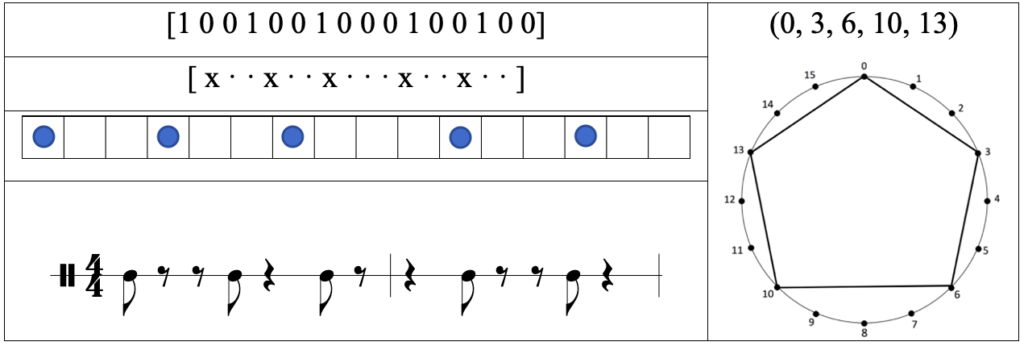
Tabla 6: Representaciones del ritmo E(5,16) con variación rítmica
4. Estudio de la teoría de los conjuntos de grados cromáticos – Pitch Class Sets
A grandes rasgos, esta teoría consiste en todo un sistema de organización de alturas en donde mediante técnicas reduccionistas, se obvian cierto número de transposiciones, inversiones y permutaciones preponderando así, las combinaciones interválicas. Estas generan conjuntos de sonidos que permitir su clasificación, manipulación e implementación en diversos análisis teóricos y como lenguaje para ser implementado en la composición musical.
En este contexto, cada sonido adopta una representación mediante un número entero universal set, siendo estos equivalentes a cualquier sonido[19] (independiente de su octava). Así mismo, estos son correspondientes enarmónicamente, obteniendo 12 Pitch Class (PC) diferentes[20], tal y como se muestra en la siguiente representación.

Tabla 7: Pitch Class y su equivalencia alfa-numérica
Un PC es elementalmente una altura que funciona como base representativa y comparable para todas las demás[21], haciendo posible la organización de conjuntos primarios que permiten ser relacionadas con sus variantes que, teóricamente, poseen las mismas características estructurales.
Al ser representaciones alfanuméricas del total cromático es posible combinar el total de sus elementos por medio de conjuntos[22], de esta manera y al realizar el proceso matemático para calcular el número de combinaciones posibles para cada conjunto, se obtiene en la sumatoria de sus resultados un total de: 4096 combinaciones[23], como se expresa a continuación.
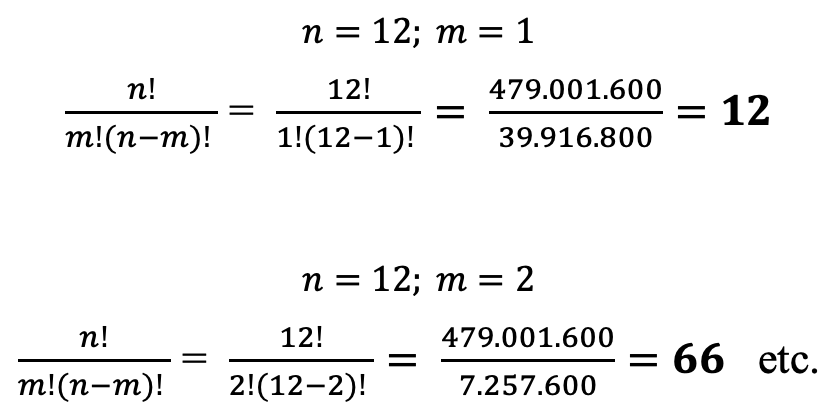
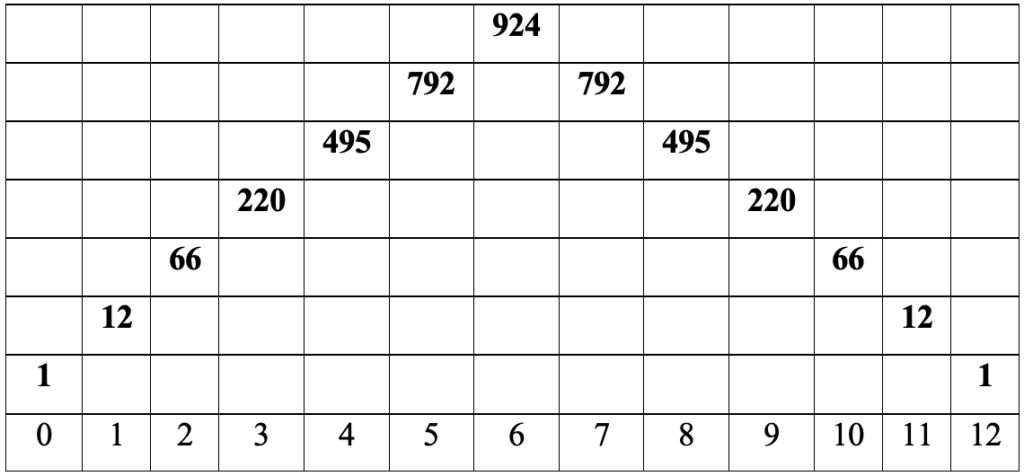
Tabla 8: Pirámide de resultados matemáticos en el proceso de combinatoriedad.
Los conjuntos obtenidos reciben el nombre de Clase de Conjunto o Set Class (SC) los cuales son esencialmente equivalentes[24] a sus variantes en transposición e inversión. La SC se identifica mediante dos números entre paréntesis (2-1), el primero indica la cantidad de elementos del conjunto número cardinal; y el segundo, se refiere a su orden dentro de lista número ordinal[25].

Tabla 9: Representación en lenguaje musical de una SC
Todos las SC que son cabezas de fila (1-1), (2-1), (3,1) … (12-1), tienen la particularidad de ser los más disonantes debido a que están conformados con un fragmento de la escala cromática, además, estos corresponden a la forma prima de cualquiera de sus variantes por estar ubicados a nivel cero[26].
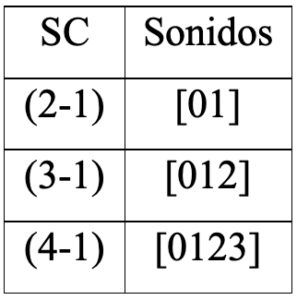
Tabla 10: Elementos de tres ejemplos de una SC
Las propiedades estructurales de cada SC están consignadas en la sección vector interválico, en donde es posible acceder individualmente a la información interválica interna, la que posteriormente será el fundamento que permitirá realizar la equivalencia con sus inversiones o transposiciones. Al vector interválico lo componen seis números que, en el orden establecido (de izquierda a derecha) indican el número de: segundas menores y mayores, terceras menores y mayores, cuartas justas y aumentadas de cada SC; de esta manera, en la siguiente ilustración, se puede observar que la SC (3-6) esta compuesta con los siguientes intervalos[27] (0 segundas menores, 2 segundas mayores, 0 tercera menor, 1 tercera mayor, 0 cuartas justas y 0 cuartas aumentadas), por lo tanto, el vector interválico de la SC (3-6) corresponde a: [020100][28]
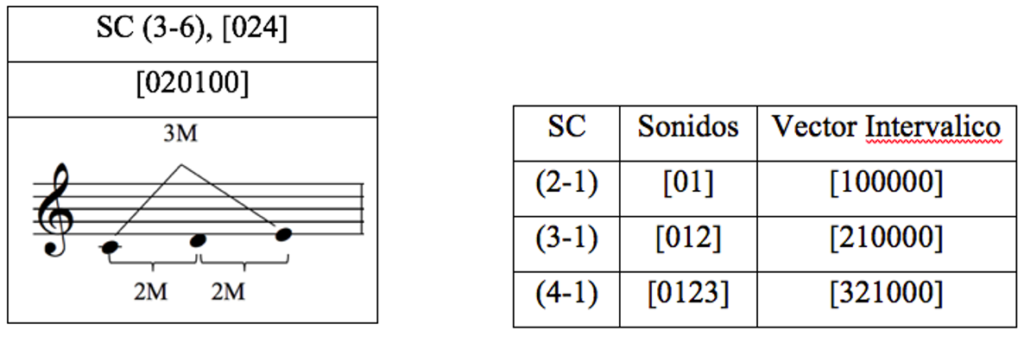
Figura 6: Ejemplos de vector interválico
Puesto que para conformar los conjuntos se toman n sonidos de doce posibles , es natural que exista un “sobrante” del total de elementos que no hacen parte de la SC, estos conformarán un conjunto que deberán ser consignados en una categoría denominada: complemento, de esta manera, las SC (4-1) y (8-1) son complementarios entre si[29].
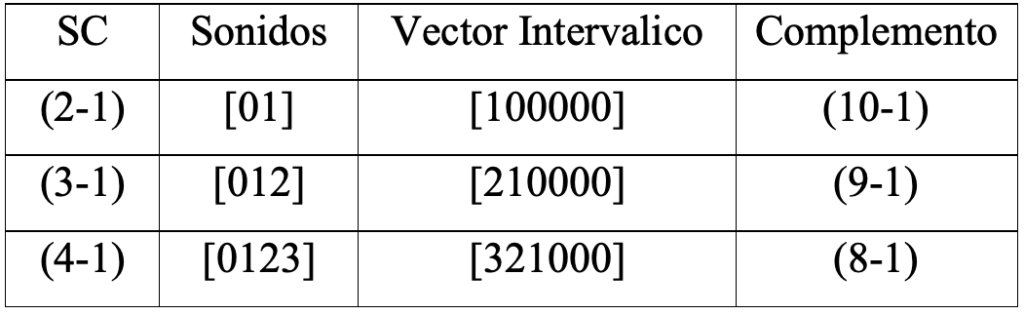
Tabla 11: Ejemplos de SC complementarios
El termino PCS[30] fue propuesto por el compositor estadounidense Milton Babbitt (1916 – 2011), como consecuancia o resultado del estudio de la teoría de la música dodecafónica. Posteriormente, fue el teórico musical estadounidense Allen Forte (1926 – 2014), quien adoptó esta teoría, ampliándola a sistemas musicales con ordenamientos diferentes al dodecafónico y al serialismo[31]. Los PCS [0,1,2] y [1,0,2] son equivalentes, puesto que presentan los mismos elementos, aunque estén en ordenes distintos unordered sets, no implica cambios sustanciales en su estructura interna; por el contrario, los conjuntos que son estructuralmente diferentes (0,1,2), (0,2,4) se consideran ordenados ordered sets puesto que, representan fundamentalmente la estructura principal, a estos se les denomina conjuntos en forma prima[32].
Para efectos del análisis y clasificación de la forma prima de una determinada SC, es implementada la staff notation. Esta consiste en la continuación de la serie de números enteros que se asignan a cada sonido de la escala inmediatamente termina la primera octava, como se observa en la siguiente imágen, al sonido Do de la segunda octava, se le ha asignado el entero 12, de esta forma continúa la serie de forma consecutiva.
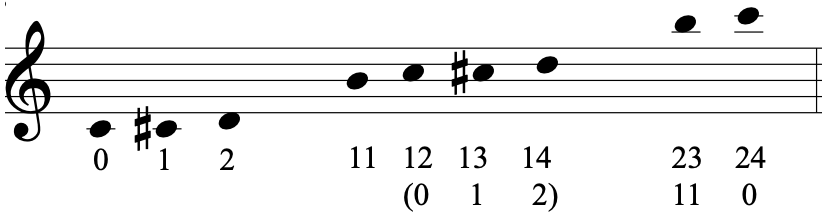
Figura 7: Staff notation
Teniendo en cuenta la información anterior, se procede a realizar los pasos siguientes para hallar la forma prima de una SC[33].
Considerese el siguiente PCS [8,9,1,2,3]
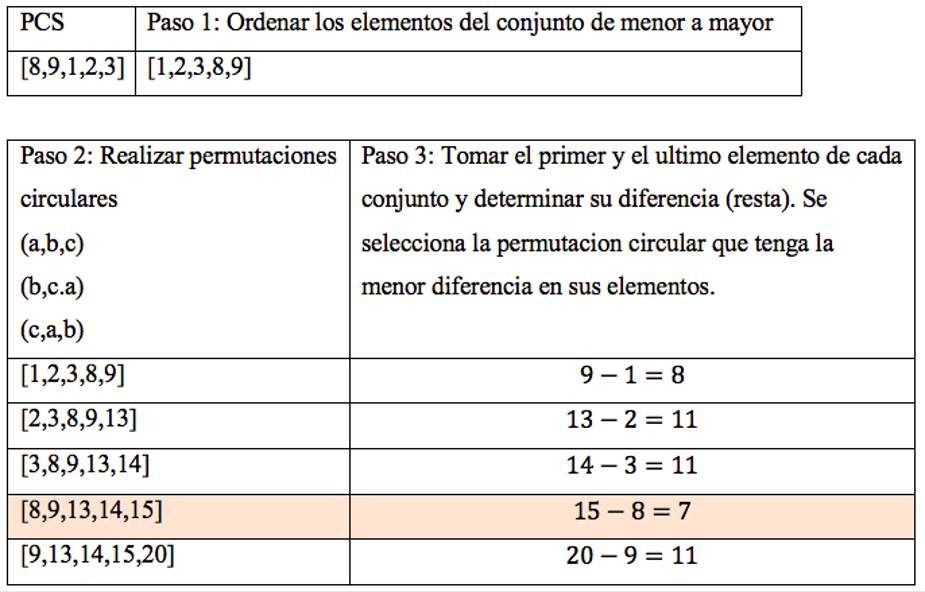

Figura 8: Proceso para hallar la forma prima de una SC.
En un análisis de conjuntos más detallado, se develan diversas organizaciones de acordes, los cuales, son clasificados obedeciendo a su nivel de consonancia y/o disonancia, sustentada en el estudio del número de cuartas aumentadas que se encuentren inmersas en su estructura, esto con el proposito de dar cierta funcionalidad a los acordes resultantes mediante momentos de tensión y distensión que generan los encadenamientos armónicos, todo esto emarcado dentro del estudio de la interválica y la altura[34]. De hecho, el análisis de conjuntos no solamente es implementado en el análisis teórico, sino que también, es una herramienta relevante en el campo compositivo, ya que permite un mayor control de sus caracteristicas estructurales y funcionales, de esta manera, es posible clasificar cada SC de acuerdo a su estructura interna, como sigue:

Tabla 12: Visualización de ejemplos de clasificación de SC y análisis de conjuntos[35]
5. Exposición del proceso creativo musical y acercamiento a la composición asistida
Para la elaboración de un ejemplo musical en donde se apliquen los conceptos anteriormente expuestos, se procederá a ser asistidos con el software Open Music[36] (OM) de manera que, el proceso creativo sea fundamentado con el material musical proporcionado por el software y los programas que conforman la librería OM-Matrix[37], a manera de herramientas que permitan simplicar drásticamente los procesos para generar el material musical y que posteriormente, se proceda a su organización artísitica en la composición, particularmente, de una pieza para piano[38].
La exposición será realizada describiendo los procesos impementados a través de OM en la evolución rítmica, la generación de material armónico, y las estructuras temáticas de la pieza para piano, señalando las herrramientas proporcionadas por el software y que fueron implementadas en el desarrollo del discurso musical. Finalmente, todo el material musical asistido por OM, será descrito e identificado de manera que, permita su posterior análisis para el fin que corresponda.
5.1 Procesos Compositivos y Evolución del Ritmo
En el contexto rítmico, se han elegido los ritmos euclidianos E(3,8) y E(3,4) correspondientes a la habanera cubana y la cumbia colombiana, respectivamente. Estos patrones deben ser “traducidos” al lenguaje matemático mediante fracciones numéricas, siendo estos los datos que recibirá y procesará OM. Para ello, se implementó el Patch interpol-ritmos el cual consiste en crear variaciones rítmicas que parten de un ritmo (a) hasta transformarse gradualmente en el ritmo (b) tal y como se muestra a continuación.
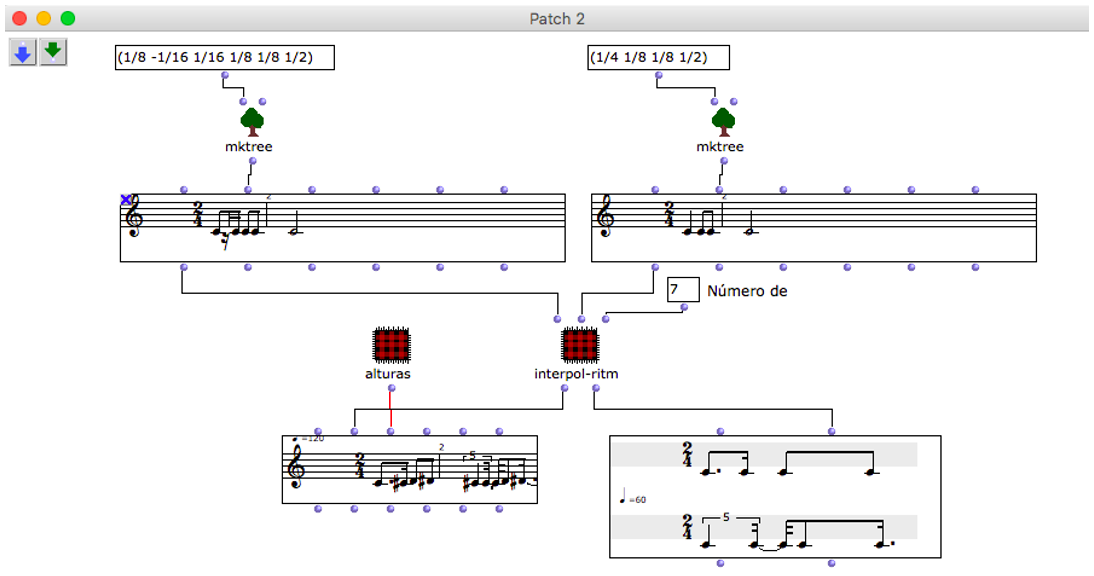
Figura 9: Interpolarización rítmica
De esta manera, se le pidió a OM que genere siete variaciones ritmicas que progresivamente serán cada vez más similares al ritmo final. En este caso el ritmo inicial es el E(3,8) y el final el E(3,4), a continuación se exponen las variaciones rítmicas asistidas por OM.

Figura 10: Evolución rítmica generada por OM
En el contexto musical, las variaciones rítmicas han sido seleccionadas de manera gradual, siendo expuestas de manera progresiva y como proceso acumulativo dentro de la pieza musical, distribuidas en los siguientes compases: c.5, c.6, c.13, c.14, c.27, c.43, c.47. Asi mismo, en los c. 23 – 26, se hace aumentación del ritmo inicial E(3,8) como recurso compositivo.
5.2 Material Armónico y Temático Fundamentado en Cadenas Cerradas
Para desarrollar este apartado, se eligieron dos números perfectos[39], el [496] único número perfecto de tres digitos y el [2,305,843,008,139,952,128] descubierto por L. Euler en 1772. Para realizar el proceso, simplemete se diseccionó el número en cifras de tres elementos, eliminando arbitrariamente el 2, quedando asi, seis grupos de tres elemetos [305] [843] [008] [139] [952] [496] (incluyendo el numero perfecto 496).
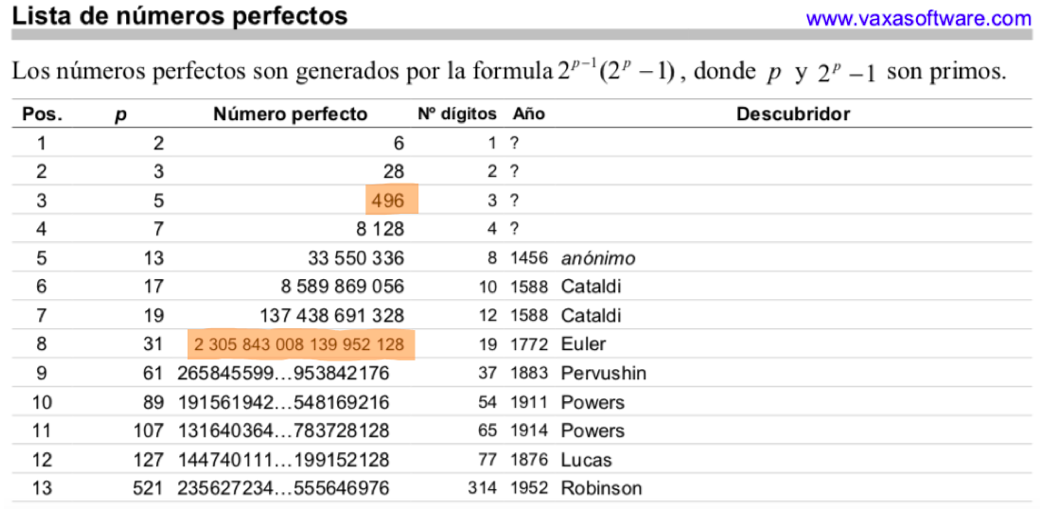
Figura 11: Listado de los primeros números perfectos
Posteriormente, se identifica a que SC pertenece cada conjunto resultante mediante el siguiente proceso en OM.
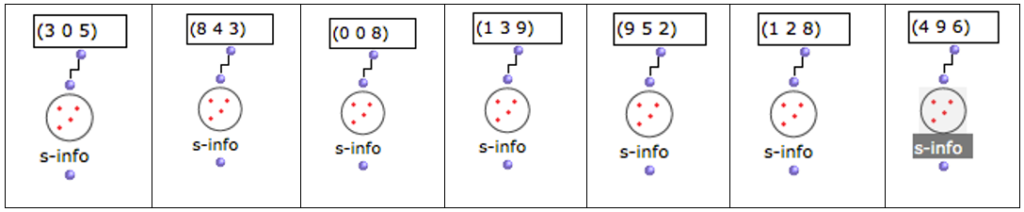
Tabla 13: Objeto s-info
Al introducir la información de cada conjunto al objeto s-info arroja la Set Class correspondiente, además de su forma prima y el vector interválico. Posteriormente, se asigna una letra a cada uno para efectos de exposición e identificación en el proceso de estructuración musical y de exposición teórica, tal y como lo muestra la tabla siguiente:
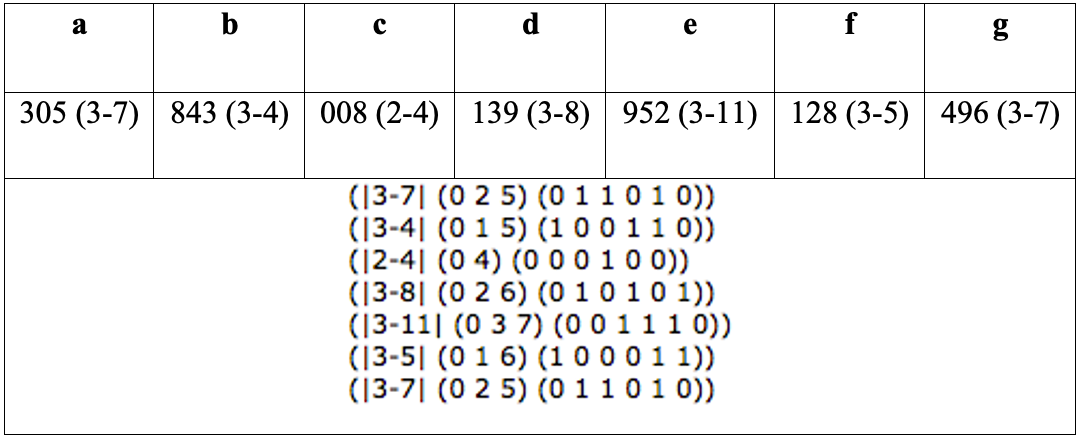
Tabla 14: Estructuración y equivalencia de los conjuntos con las SC
Una vez teniendo la información de la SC de cada conjunto, se procede a generar series de sonidos asistido por OM, los cuales serán el material para la organización armónica y temática o melódica, si se quiere. Para ello se utiliza el objeto closed-chains que produce cadenas cerradas de sonidos alimentadas por los elementos pertenecientes a una determinada SC[40]. En la imagen se introdujo los elementos [0 2 5] que conforman la SC (3-7).

Tabla 15: Cadenas cerradas resultantes
A cada elemento de cada serie arrojada por el software se le es asignado (de manera aleatoria) un sonido según la organización MIDI, cada serie podrá ser usada de manera original o también de forma invertida y/o transportada, siendo necesario utilizar el objeto s-transform como se expone a continuación:
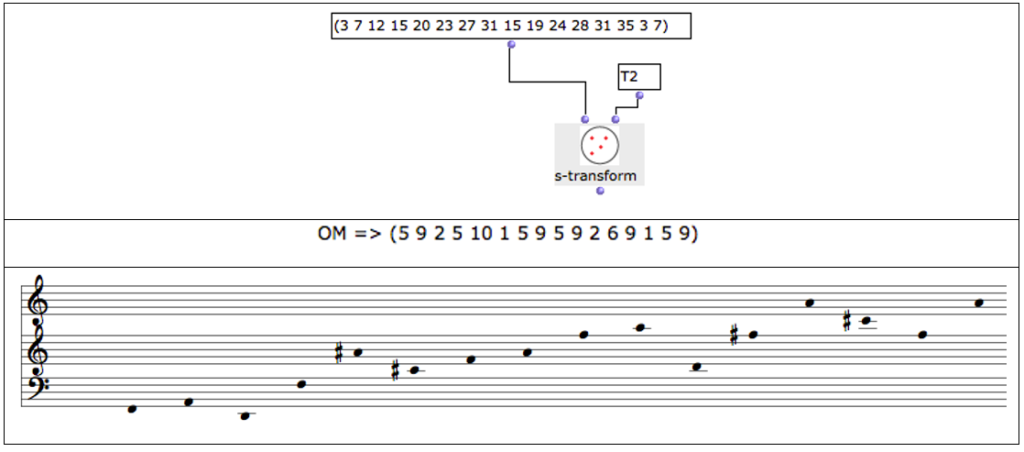
Tabla 16: Serie eT2
De la misma manera, y como se observa en la siguiente imagen, en lugar de alimentar el objeto con los valores pertenecientes a la forma prima, se ingresan los elementos del número perfecto original [843], simplemente se trata de intercalar los elementos de las formas primas y los elementos de los conjuntos organizados con los números perfectos con el propósito de enriquecer la sonoridad de los acordes que resulten del proceso asistido.
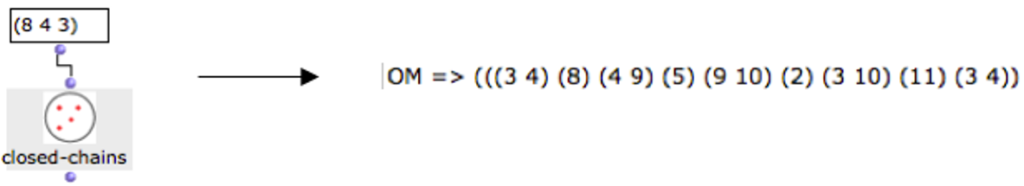
Figura 12: Cadenas cerradas generadas con OM
Una vez teniendo una gran variedad de series de sonidos, es posible realizar construcciones armónicas que serán procedentes de cada serie, para realizar este proceso se implementa el patch campos-armónicos, ya que al ingresar los elementos de las series, ya sea en su forma original, en inversión y/o transposición, generan diversos acordes que son producto en principio, de los conjuntos elaborados con los números perfectos. En cuanto a los acordes que son asistidos por OM, se respetarán al máximo la disposición, el registro y el número de sonidos resultantes de cada bloque de acordes.
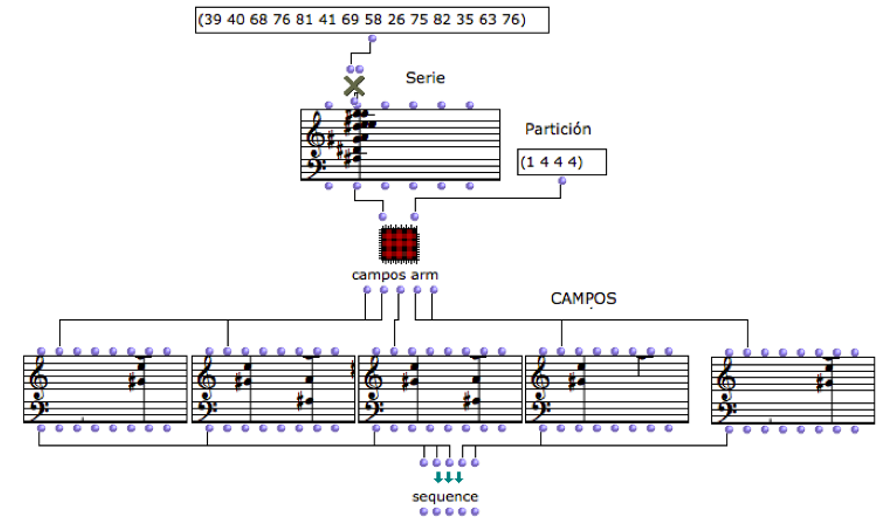
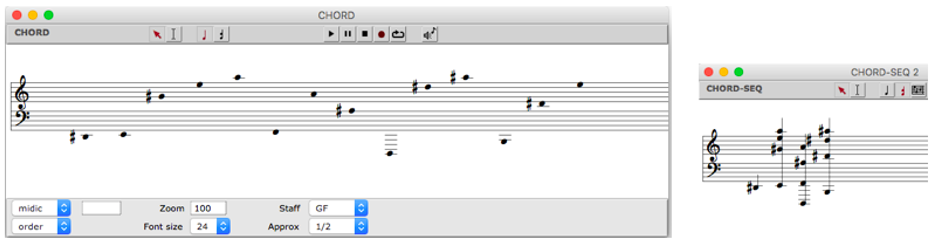
Figura 13: Material armónico generado por OM
A grandes rasgos, OM generó cinco acordes y una serie por cada conjunto de números perfectos (sin contar inversiones y transposiciones) de diversos regístros y texturas. Como se aprecia, OM no es más que una herramienta que produce variadisimo y abundante material musical con el cual se deberá constituir, en este caso, una pieza para piano. Todas las series y los recursos utilizados para la composición de esta obra para piano Génesis están condensadas en la siguiente ilustración.
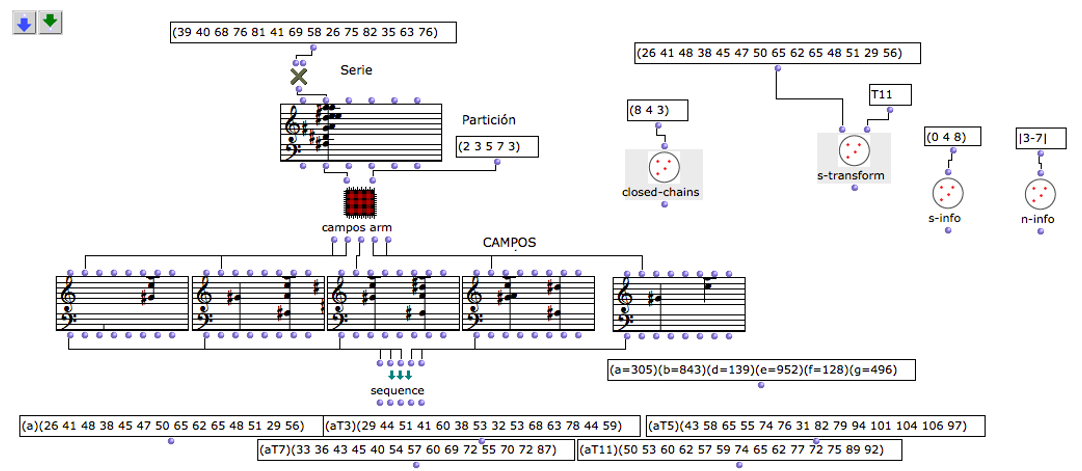

Figura 14: Recursos musicales implementados y generados por OM
5.3 Desarrollo de la Forma Musical y Descripción del Material Usado por Compás
La organización de esta pieza musical esta pensada de tal forma que, se avance progresivamente y en su orden desde la primera serie (a) hasta la ultima (g) asi, a medida que avanza el discurso musical, se incrustan inversiones y transposiciones, variando notoriamente la sonoridad. Además, las ultimas series (e, f, g) presentan mayor cantidad de elementos (sonidos), por ende, la textura de los acordes será mucho más densa, hasta el punto del cluster.
En cuanto a la forma musical, se da utilidad a lo expuesto anteriormente para construirla en relación con la “funcionalidad” de los acordes, entendiendolo desde el punto de vista del estudio de las alturas y no desde el concepto tradicional tonal. Es obvio que el material musical asistido por OM no tiene relación tonal, pero es importante generar momentos de tensión-distensión y cierto movimiento e interacción conforme avance la música. De esta manera, surge una forma ternaria simple (A B A`) en donde la sección A expone un tematismo con acordes provenientes de las primeras series; en la sección B, es desarrollado con acordes mucho más densos y desarrollo rítmico y finalmente; en la sección A` presenta recapitulación con ciertas variaciones con carácter de coda.
En el siguiente esquema se exponen las series utilizadas en cada uno de los compases de la pieza musical, las series invertidas y/o transpuestas, la procedencia de los acordes resultantes y la delimitación por secciones de la forma musical.
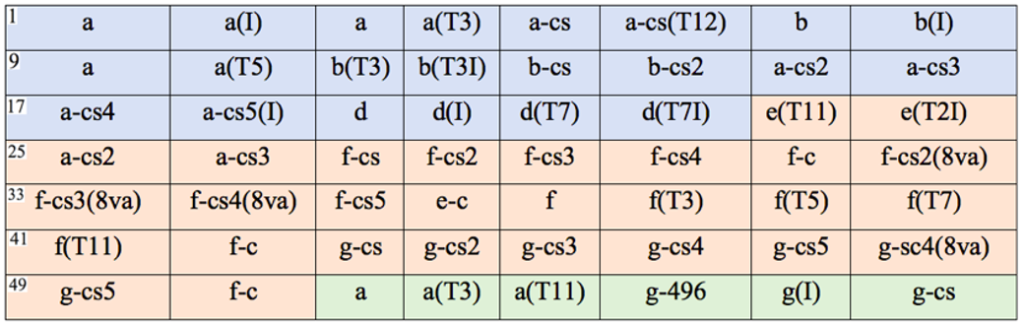
Figura 15: Esquema de la forma musical y exposición de los recursos implementados por compás
BIBLIOGRAFÍA
Cadavieco Castillo, Manuel J. 2002. «Pitágoras y los números perfectos.» Ingeniería (Universidad Autónoma de Yucatán) 6 (2): 47-49.
Cetta, Pablo, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
Cetta, Pablo. 2004. «Principios de Estructuración de la Altura Empleando Conjuntos de Grados Cromáticos.» Altura-Timbre-Espacio. Cuaderno de Estudi Nº5. IIMCV. Educa.
Cetta, Pablo. 2018. Fundamentos de Composición Musical Asistida en el entorno de programación OpenMusic. Ciudad Autónoma de Buenos Aires: Instituto de Investigación Musicológica «Carlos Vega»; Pontificia Universidad Católica Argentina.
Demaine, Erik D., Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, y David R. Wood. 2009. «The distance geometry of music.» Computational Geometry 429-454.
Forte, Allen. s.f. The Structure of Atonal Music. Yale, United States of America: Yale University, Courier Companies.
Gómez-Martín, Francisco, Perouz Taslakian, y Godfried Toussaint. 2009. «Interlocking and Euclidean rhythms.» Journal of Mathematics and Music 3 (1): 15-30.
Gómez, Paco. s.f. «El algoritmo de Euclides como principio musical.» Articulo. Madrid.
Liern Carrión, Vicente. 2019. «Música y Matemáticas.» Taller: Música y Matemáticas. Manizales, Caldas, Colombia.
O`Conor, J J, y E F Robertson. 1999. MT Mac Tutor. Enero. Último acceso: 25 de Marzo de 2021. https://mathshistory.st-andrews.ac.uk/Biographies/Euclid/.
Rusiñol, Mª Carmen. 2017. Pitágoras, números armonía y esferas. Sevilla – España: PUNTO ROJO LIBROS, S.L.
s.f. Lecture 5: Euclid`s algorithm Introduction . Último acceso: 25 de Marzo de 2021. http://www.macs.hw.ac.uk/~markl/teaching/CODES/L5.pdf.
Schuijer, Michiel. 2008. Analyzing Atonal Music Pitch-Class Set Theory and Its Contexts. Editado por University of Rochester Press. Rochester, NY.
Shallit, Jeffrey. 1994. «Origins of the Analysis of the Euclidean Algorithm.» HISTORIA MATHEMATICA 21 401-419.
Toussaint, Godfried. «The Euclidean Algorithm Generates Traditional Musical Rhythms.» School of Computer Science, McGill University. Montréal, Québec, Canada.
Toussaint, Godfried. 2002. «A Mathematical Analysis of African, Brazilian and Cuban Clave Rhythms.» Proceedings of BRIDGES: Mathematical Conections in Art, Music and Science, Towson University. Towson, 27-29 de July.
El presente artículo fue realizado en el marco del seminario: Matemática Aplicada a la Composición Musical de la Pontificia Universidad Católica de Argentina, bajo la orientación del Doctor en Música, Pablo Cetta.
NOTAS
[1] Mª Carmen Rusiñol. 2017. Pitágoras, números armonía y esferas. Sevilla – España: PUNTO ROJO LIBROS, S.L.
[2] Pitch Class Sets, en las fuentes bibliográficas en Inglés.
[3] Realizando este proceso de forma numérica, se debe tener en cuenta que, al dividir los segmentos y obtener un nuevo divisor, estos deben ser divisibles con los demás divisores que se obtengan durante el proceso de calculo del MCD.
[4]Vicente Liern Carrión. 2019. «Música y Matemáticas.» Taller: Música y Matemáticas. Manizales, Caldas, Colombia.
[5] Destacadísimo matemático de la antigua civilización Greco-Romana, conocido principalmente por su libro The Elements. Fue el filósofo Proclo quien consigno entre sus escritos algunos datos biográficos de Euclides, siendo estos los únicos que se conocen. O`Conor, J J, y E F Robertson. 1999. MT Mac Tutor. Enero. Último acceso: 25 de Marzo de 2021. https://mathshistory.st-andrews.ac.uk/Biographies/Euclid/.
[6]Jeffrey Shallit. 1994. «Origins of the Analysis of the Euclidean Algorithm.» HISTORIA MATHEMATICA21 401-419.
[7] Jeffrey Shallit. 1994. «Origins of the Analysis of the Euclidean Algorithm.» HISTORIA MATHEMATICA21 401-419.
[8] s.f. Lecture 5: Euclid`s algorithm Introduction . Último acceso: 25 de Marzo de 2021. http://www.macs.hw.ac.uk/~markl/teaching/CODES/L5.pdf.
[9] Francisco Gómez-Martín, Perouz Taslakian, y Godfried Toussaint. 2009. «Interlocking and Euclidean rhythms.» Journal of Mathematics and Music 3 (1): 15-30.
[10] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, y David R. Wood. 2009. «The distance geometry of music.» Computational Geometry 429-454.
[11] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, y David R. Wood. 2009. «The distance geometry of music.» Computational Geometry 429-454.
[12] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, y David R. Wood. 2009. «The distance geometry of music.» Computational Geometry 429-454.
[13] De la misma manera, si las secuancias de un bit “sobrantes” son unos, se debera realizar el mismo proceso de adición a las secuencias de dos o mas bits.
[14] Erik D. Demaine, Francisco Gomez-Martin, Henk Meijer, David Rappaport, Perouz Taslakian, Godfried T. Toussaint, Terry Winograd, y David R. Wood. 2009. «The distance geometry of music.» Computational Geometry 429-454.
[15] Godfried Toussaint. 2002. «A Mathematical Analysis of African, Brazilian and Cuban Clave Rhythms.» Proceedings of BRIDGES: Mathematical Conections in Art, Music and Science, Towson University. Towson, 27-29 de July.
[16] Godfried Toussaint. 2002. «A Mathematical Analysis of African, Brazilian and Cuban Clave Rhythms.» Proceedings of BRIDGES: Mathematical Conections in Art, Music and Science, Towson University. Towson, 27-29 de July.
[17] El proceso matemático aplicado al ritmo E (5, 16) Bossa Nova arroja la siguiente secuencia binaria: [1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 0] (Tabla 5), sin embargo, el ritmo que se suele implementar en la práctica se obtiene si se toma la secuencia desde el tercer ataque como punto de partida del patrón rítmico, de la manera que sigue: [1 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0] (Tabla 6).
[18]Godfried Toussaint. «The Euclidean Algorithm Generates Traditional Musical Rhythms.» School of Computer Science, McGill University. Montréal, Québec, Canada.
[19]Allen Forte. s.f. The Structure of Atonal Music. Yale, United States of America: Yale University, Courier Companies.
[20] También llamada notación de enteros, concepto que viene de la música atonal donde los sonidos enarmónicos son equivalentes sin que necesariamente sea una notación arbitraria, sino que es independiente de cualquier otra.
[21] Allen Forte. s.f. The Structure of Atonal Music. Yale, United States of America: Yale University, Courier Companies.
[22] Los conjuntos 0 y 12, incluidos en la tabla, se les denomina conjunto nulo y agregado, respectivamente.
[23]Pablo Cetta, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
[24] Los conjuntos [0,2,4], [0,A,8],[7,9,B] son equivalentes ya que presentan la misma estructura interválica, solo que se trata de su forma prima, de su inversión y transposición, respectivamente; por ende, todos los conjuntos mencionados pertenecen a la misma Set Class (3-6).
[25] Pablo Cetta, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
[26] Pablo Cetta. 2004. «Principios de Estructuración de la Altura Empleando Conjuntos de Grados Cromáticos.» Altura-Timbre-Espacio. Cuaderno de Estudi Nº5. IIMCV. Educa.
[27] Es importante diferenciarlos entre ellos, puesto que los intervalos de: séptima y novena, pertenecerían a la misma clase interválica de segunda ya que, en síntesis, este ultimo representa su mínima expresión a la inversión y de un intervalo compuesto, respectivamente.
[28] Pablo Cetta. 2004. «Principios de Estructuración de la Altura Empleando Conjuntos de Grados Cromáticos.» Altura-Timbre-Espacio. Cuaderno de Estudi Nº5. IIMCV. Educa.
[29] Pablo Cetta, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
[30] El término Basic Shape, fué implementado en primera instancia, sin embargo, fue reemplazado por Pitch Class Set, ya que el primero se desarrolla en el marco de la serie dodecafónica y el segundo, es mucho más general. Schuijer, Michiel. 2008. Analyzing Atonal Music Pitch-Class Set Theory and Its Contexts. Editado por University of Rochester Press. Rochester, NY.
[31] Michiel Schuijer. 2008. Analyzing Atonal Music Pitch-Class Set Theory and Its Contexts. Editado por University of Rochester Press. Rochester, NY.
[32]Allen Forte. s.f. The Structure of Atonal Music. Yale, United States of America: Yale University, Courier Companies.
[33]Pablo Cetta, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
[34]Pablo Cetta, y Pablo Di Liscia. 2010. Elementos de Contrapunto Atonal. Buenos Aires, Argentina: Editorial de la Universidad Católica Argentina.
[35]Pablo Cetta. 2004. «Principios de Estructuración de la Altura Empleando Conjuntos de Grados Cromáticos.» Altura-Timbre-Espacio. Cuaderno de Estudi Nº5. IIMCV. Educa.
[36] Lenguaje de programación visual basado en Lisp http://repmus.ircam.fr/openmusic/home
[37] Cetta, Pablo. 2018. Fundamentos de Composición Musical Asistida en el entorno de programación OpenMusic. Ciudad Autónoma de Buenos Aires: Instituto de Investigación Musicológica «Carlos Vega»; Pontificia Universidad Católica Argentina.
[38] Los elementos dados por OM provienen de algunos objetos estudiados en el seminario de Matemática Aplicada a la Música, siendo ellos de tipo rítmico, armónico y series de cadenas cerradas, con el proposito de estudiar su funcionamiento.
[39] A grandes rasgos, son enteros positivo que se obtiene cuando la sumatoria de sus divisores dan exactamente el mismo número, ej: 1 + 2 + 3 = 6. Manuel J. Cadavieco Castillo. 2002. «Pitágoras y los números perfectos.» Ingeniería (Universidad Autónoma de Yucatán) 6 (2): 47-49.
[40] Cada serie se identifica con la letra que fue asignada a cada conjunto de números perfectos.
